Nochmal Exponentialrechnung

Weil mir so viele Leser schrieben, der Anstieg der Infektionen sei doch tatsächlich linear:

Nein. Ich will Euch zeigen, warum.

Kam übrigens vorhin in den Nachrichten: Die Verdopplungszeit hat sich nur durch die Isolation gedehnt, wenn ich mich recht erinnere, sagten sie was von 14 oder 14,5 Tagen. Es gibt immer noch eine Verdopplungszeit.

Man sollte sich davor hüten, etwas für linear zu halten, nur weil es gerade mal ein paar Tage ungefähr gerade aussieht. Exponentialkurven können – je nach Basis – in der x-Achse sehr gedehnt aussehen und für das Auge annähernd linear erscheinen.

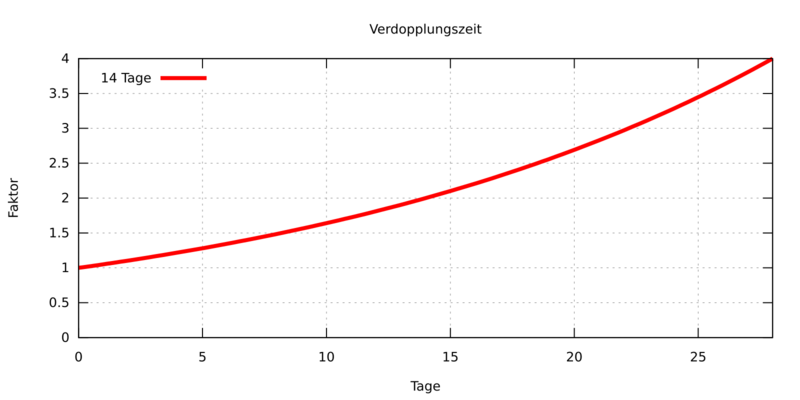
Das gilt vor allem dann, wenn man die Basis (Verdopplungszeit) innerhalb der Kurve verändert, wenn man das also aufzeichnet und links mit einer Verdopplungszeit von 5 Tagen anfängt (2^x/5) und nach rechts hin die Verdopplungszeit dehnt (2^x/14). Das sieht dann linear aus, weil man immer flachere Exponentialfunktionen miteinander mischt, aber dass es eine Exponentialfunktion ist, kann man damit auch nicht ändern. Damit behummst man sich selbst.

Oder anders gesagt: Ja, eine Exponentialkurve kann durchaus völlig gerade und linear aussehen, wenn man die x- oder y-Achse unterschiedlich stark dehnt. Sowas macht man beispielsweise, wenn man logarithmische Achsen aufzeichnet (als man früher noch mit Tuschefüller auf Millimeterpapier zeichnete, gab es für so etwas extra Logarithmenpapier zu kaufen) Mit sowas kann man tatsächlich eine Exponentialfunktion als Gerade zeichnen, weil es durch die nicht-linearen Maßstäbe zur Gerade (nicht nur ungefähr, sondern wirklich eine Gerade) wird, siehe den verlinkten Artikel. Nur weil etwas wie eine Gerade aussieht, ist es noch lange keine lineare Funktion, denn das gilt nur, wenn die Achsen lineare (oder gleich verzerrte) Skalen haben. Genau das macht man nämlich, die Skala verzerren, wenn man mitten in der Funktionsdarstellung mal stillschweigend die Basis wechselt.

Wenn man aber während der Pandemie durch Maßnahmen eingreift, die durch Isolation die Verdopplungszeit dehnen, also den Skala der X-Achse nichtlinear verzerren, sondern mittendrin nahezu verdreifachen, kann man nicht sagen, der Anstieg sei linear, weil es so gerade aussieht.

Natürlich kann man sagen, dass einen die Mathematik nicht interessiert, weil man zufrieden damit ist, dass der Anstieg über die Zeit linear aussieht. Ist doch schön. Ja, ist schön. Bleibt aber nur so, indem man weiter auf dieselbe Weise trickst und die Basis, also die Verdopplungszeit, immer weiter dehnt, die Maßnahmen also immer weiter verschärft, damit sich der Kurventrick wiederholt.

Fallt nicht auf jede Statistik und Kurvengraphik rein.